Question

the digits 1through 6 are used for a set of locker codes. suppose the digits cannot repeat. find the number of possible two digit codes and three digit codes. describe any pattern and use it to predict the number of possible five digit codes

Answer 1

the answer of this question is 720 ways

Answer 2

This is a permutation problem.

a) To find the number of possible two digits codes

`^6P_2`
`^6P_2=(6!)/((6-2)!)`
`\begin{gathered} =(6!)/(4!) \\ =(720)/(24) \\ =30\text{ ways} \end{gathered}`

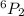
There are 30 possible two-digit codes pattern.

b) To find the number of three digits codes

`\begin{gathered} ^6P_3=\text{ }(6!)/((6-3)!) \\ \text{ =}(6!)/(3!) \\ \text{ =}(720)/(6) \\ \text{ = 120 ways} \end{gathered}`

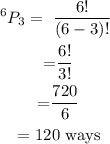
There are 120 possible three-digit codes pattern.

Any other pattern can be calculated using

`\begin{gathered} ^6P_r \\ \text{where r is the number of digits code (1,2,3,4,5,6)} \end{gathered}`

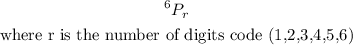
So to predict the number of possible five-digit codes will be:

`^6P_5`
`\begin{gathered} =(6!)/((6-5)!) \\ =(6!)/(1!) \\ =720\text{ways} \end{gathered}`

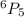
There are 720 different possible five-digit codes