SOLUTION:
Step 1:
In this question, we have the following:
In the picture below, measure 1 is (5x-14) degrees and measure 3 is (2x+10) degrees.
Find the measure of 2.
Step 2:
From the diagram, we can see that angles 1 and 3 are vertically opposite and they are also equal.
Based on this fact, we can see that:
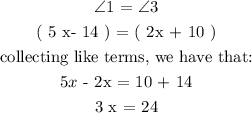
Divide both sides, we have that:

Then, we put x = 8 into the equation for Angle 1 , we have that:
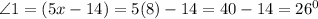
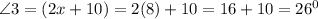
Hence, we can see that Angles 1 and 3 are equal.
Step 3:
From the diagram, we can see that:
we can see that angles 2 and 4 are vertically opposite and they are also equal.
Recall that angles 1 and 3 are also vertically opposite and they are also equal.
Therefore, we can see that:
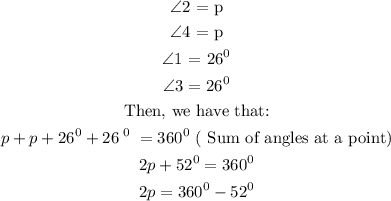
Divide both sides by 2, we have that:

CONCLUSION:
![\begin{gathered} \operatorname{Re}call\text{ that }\angle2\text{ = p} \\ \text{Then, we have that:} \\ \angle2=154^0 \end{gathered}]()