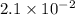Answer : The correct option is, (A)
Solution : Given,
Concentration of
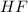 =
=
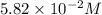
Concentration of
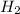 =
=
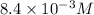
Concentration of
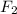 =
=
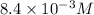
The given balanced equilibrium reaction is,
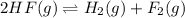
The expression for equilibrium constant will be,
![K_(eq)=([H_2]* [F_2])/([HF]^2)](https://img.qammunity.org/2018/formulas/chemistry/high-school/267wws2ogpd26fyk56zx1gtil5arsfkdd1.png)
Now put all the given values in this formula, we get
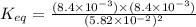
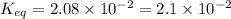
Therefore, the value of equilibrium constant is,