Question

How do you create a truth table to prove that for any statement, p,~(~p) equals p?

Answer 1

If
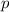
`p` is true, then
`\sim p` is false, which in turn means
`\sim(\sim p)` is true.

If
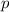
`p` is false, then
`\sim p` is true, and so
`\sim(\sim p)` is false.

So, because
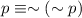
`p\equiv\sim(\sim p)` in both cases, the statement is a tautology (always true).

If you were to put this in a table, you would have one column each for
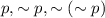
`p,\sim p,\sim(\sim p)`. In the first column (
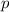
`p`) you can think of
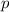
`p` as an independent variable that can only take two values, true and false. In the next column (
`\sim p`), you would negate the value in the previous column. And so on.

It should roughly look like this:

p ... ~p ... ~(~p)
T ... F ... T
F ... T ... F