Let x be the velocity (rate of change ) of one of the buses. We know that the other one travels 16 km/h slower; this means that the second velocity is:

Now the combined velocity would be:
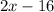
We know that the distance is equal to time by velocity, then we have that:
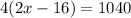
Solving for x we have:
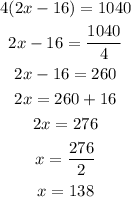
Therefore the rate of the faster bus is 138 km/h and the rate for the slower bus is 122 km/h.