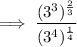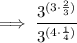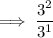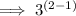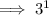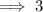Question

Please answer this question​

Answer 1

Given that,

→ ((14² - 13²)^⅔)/((15² - 12²)^¼)

Evaluating the problem,

→ ((14² - 13²)^⅔)/((15² - 12²)^¼)

→ ((196 - 169)^⅔)/((225 - 144)^¼)

→ (27^⅔)/(81^¼)

→ ((3³)^⅔)/((3⁴)^¼)

→ (3²)/3

→ 9/3 = 3

Therefore, the solution is 3.

Answer 2

3

Explanation:

Given expression:

`\frac{(14^2-13^2)^{(2)/(3)}}{(15^2-12^2)^{(1)/(4)}}`

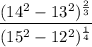
Following the order of operations, carry out the operations inside the parentheses first.

Apply the Difference of Two Square formula
`x^2-y^2=\left(x+y\right)\left(x-y\right)`

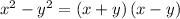
to the operations inside the parentheses in both the numerator and denominator:

`\implies \frac{((14+13)(14-13))^{(2)/(3)}}{((15+12)(15-12))^{(1)/(4)}}`

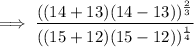
Carry out the operations inside the parentheses:

`\implies \frac{((27)(1))^{(2)/(3)}}{((27)(3))^{(1)/(4)}}`

`\implies \frac{(27)^{(2)/(3)}}{(81)^{(1)/(4)}}`

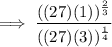
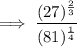
Carry out the prime factorization of 27 and 81.

Therefore, rewrite 27 as 3³ and 81 as 3⁴:

`\implies \frac{(3^3)^{(2)/(3)}}{(3^4)^{(1)/(4)}}`

`\textsf{Apply exponent rule} \quad (a^b)^c=a^(bc):`

`\implies \frac{3^{(3 \cdot (2)/(3))}}{3^{(4 \cdot (1)/(4))}}`

`\implies (3^2)/(3^1)`

`\textsf{Apply exponent rule} \quad (a^b)/(a^c)=a^(b-c):`

`\implies 3^((2-1))`

`\implies 3^1`

`\implies 3`