Question

What is the simplified form of the quantity 4 z squared minus 16z plus 15 over the quantity 2 z squared minus 11 z plus 15?

Answer 1

Factor the numerator and denominator to get
(2z-3)(2z-5) / (z-3)(2z-5)
Since there is a common factor of (2z -5) on the numerator and denominator this factor will cancel leaving (2z-3)/(z-3)

Answer 2

`((2z-3))/((z-3))`

Explanation:

`(4z^2-16z+15)/(2z^2-11z+15)`

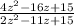
To simplify this we factor the numerator and denominator separately

factor 4z^2 - 16z+15

We apply 'ac' method, 4* 15 = 60

-10 * -6 = 60

-10 - 6 = -16

Now we split -16z using factors -10z -6z

`4z^2 - 10z-6z+15`

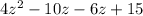
Take out GCf from first two terms and last two terms

`2z(2z-5)-3(2z+5)`

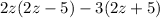
(2z-3)(2z-5)

factor 2z^2 - 11z+15

We apply 'ac' method, 2* 15 = 30

-5 * -6 = 30

-5 - 6 = -11

Now we split -11z using factors -5z -6z

`2z^2 - 5z-6z+15`

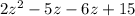
Take out GCf from first two terms and last two terms

`z(2z-5)-3(2z-5)`

(z-3)(2z-5)

Now we replace the factors

`((2z-3)(2z-5))/((z-3)(2z-5))`

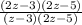
Cancel out 2z-5 at the top and bottom

`((2z-3))/((z-3))`