Question

What are the solutions of the equation (2x + 3)2 + 8(2x + 3) + 11 = 0? Use u substitution and the quadratic formula to solve.

Answer 1

The Answer is B.

Just got it right

Answer 2

`x=-2.38`

`x=-4.62`

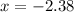
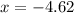
Explanation:

The question is
`(2x+3)^2+8(2x+3)+11=0`

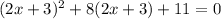
We let
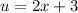`u=2x+3`, so the equation becomes:

`u^2+8u+11=0`

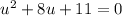
Where
`a=1, b=8, c=11`

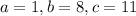
Putting it in the quadratic formula, we have:

Quadratic formula:
`(-b+-√(b^2-4ac) )/(2a)`

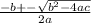
Substituting we have:
`(-8+-√((8)^2-4(1)(11)) )/(2(1))\\=(-8+-√(20) )/(2)\\=(-8+-2√(5) )/(2)\\=-4+√(5), -4-√(5) }`

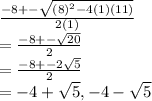
We let
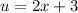`u=2x+3`, so x is:

`u=2x+3\\(-4+√(5))=2x+3\\x=(-7+√(5))/(2)=-2.38`

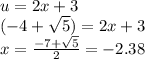
and

`u=2x+3\\(-4-√(5))=2x+3\\x=(-7-√(5))/(2)=-4.62`

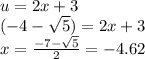
The solutions of the equation is
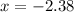`x=-2.38` (rounded to 2 decimal places), and
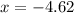`x=-4.62` (rounded to 2 decimal places)