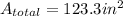Question

The figure shown is made up of a triangle and a square. The perimeter of the figure is 56 inches. What is the area of the figure? Explain.

Answer 1

`A_(total)=123.3in^(2)`

Explanation:

If the triangle and the square have the same sides, then that triangle is equilateral, that is, all its sides are the same.

Now, this is a composite shape, where one side of the triangle is on one side of the square, this means that the perimeter is the sum of all 6 sides. So, each side is

`P=6s\\56=6s\\s=(56)/(6)=9.3in`

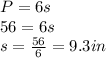
So, the area of the square is

`A_(square)=s^(2)=(9.3)^(2) =86.5in^(2)`

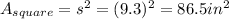
Now, the are of an equilateral triangle is

`A_(triangle)=(√(3) )/(4)s^(2)`

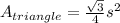
Where
`s` is the side, replacing its value, we have

`A_(triangle)=(√(3) )/(4)(9.3)^(2)=36.8in^(2)`

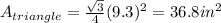
The total are of the composite figure would be the sum of each

`A_(total)= 86.5+36.8=123.3in^(2)`

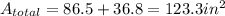
Therefore, the area of the composite shape is

`A_(total)=123.3in^(2)`