Answer:
For 1: The velocity of Ball B is 10m/s and is moving in left direction.
For 2: The velocity of Ball D is 30m/s and is moving in right direction.
For 3: The mass of Ball F is 30 kg.
Step-by-step explanation:
Let us assume that ball moving in left direction has a negative sign and the ball moving in right direction has a positive sign.
In collision reaction, the momentum remains conserved. The equation for this follows:

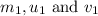 = mass, initial velocity and final velocity of ball A
= mass, initial velocity and final velocity of ball A
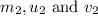 = mass, initial velocity and final velocity of ball B.
= mass, initial velocity and final velocity of ball B.
We are given:

Putting values in above equation, we get:
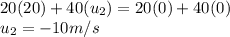
The velocity of Ball B is 10m/s and is moving is left direction.
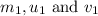 = mass, initial velocity and final velocity of ball C
= mass, initial velocity and final velocity of ball C
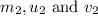 = mass, initial velocity and final velocity of ball D.
= mass, initial velocity and final velocity of ball D.
We are given:
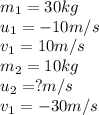
Putting values in above equation, we get:
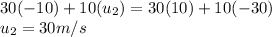
The velocity of Ball D is 10m/s and is moving is right direction.
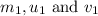 = mass, initial velocity and final velocity of ball E
= mass, initial velocity and final velocity of ball E
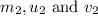 = mass, initial velocity and final velocity of ball F.
= mass, initial velocity and final velocity of ball F.
We are given:
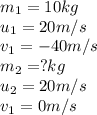
Putting values in above equation, we get:

The mass of Ball E is 30kg.