Question

I really really really need help!!!!

Answer 1

For
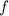
`f` to be continuous at
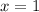
`x=1`, you need to have the limit from either side as
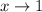
`x\to1` to be the same.


`\displaystyle\lim_(x\to1^-)f(x)=\lim_(x\to1^-)(|x-1|+2)=2`

`\displaystyle\lim_(x\to1^+)f(x)=\lim_(x\to1^+)(ax^2+bx)=a+b`

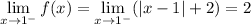
If
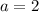
`a=2` and
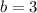
`b=3`, then the limit from the right would be
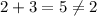
`2+3=5\\eq2`, so the answer to part (1) is no, the function would not be continuous under those conditions.

This basically answers part (2). For the function to be continuous, you need to satisfy the relation
`a+b=2`.

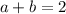
Part (c) is done similarly to part (1). This time, you need to limits from either side as
`x\to2` to match. You have


`\displaystyle\lim_(x\to2^-)f(x)=\lim_(x\to2^-)(ax^2+bx)=4a+2b`

`\displaystyle\lim_(x\to2^+)f(x)=\lim_(x\to2^+)(5x-10)=0`

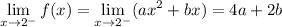
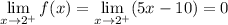
So,
`a` and
`b` have to satisfy the relation
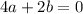
`4a+2b=0`, or
`2a+b=0`.

Part (4) is done by solving the system of equations above for
`a` and
`b`. I'll leave that to you, as well as part (5) since that's just drawing your findings.