Question

[50 POINTS] Can someone please help??

Answer 1

Width = 21.75 m

Length = 21.75 m

Explanation:

The last two digits of your student number are 37.

Therefore, the length of fencing we will work with is 37 + 50 = 87 m.

The perimeter of a rectangle is twice the sum of its width (w) and length (l). Therefore, if the total length of fencing is 87 m, the equation for the perimeter of the rectangular fence is:

`\textsf{Perimeter}=2(w+l)=87`

Rearrange the equation to isolate length (l):

`\begin{aligned}2(w+l)&=87\\\\w+l&=(87)/(2)\\\\l&=(87)/(2)-w\end{aligned}`

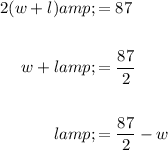
The area of a rectangle is the product of its width (w) and length (l):

`\textsf{Area}=wl`

Substitute the expression for length into the area formula to create an equation for area with respect to width only:

`\begin{aligned}\textsf{Area}&=wl\\\\&=w\left((87)/(2)-w\right)\\\\&=(87)/(2)w-w^2\end{aligned}`

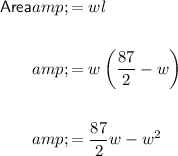
To find the width that will maximize the area, differentiate the equation for area with respect to w, set it zero, and solve for w:

`\frac{\text{d}A}{\text{d}w}=1 \cdot (87)/(2)w^(1-1)-2 \cdot w^(2-1)`

`\frac{\text{d}A}{\text{d}w}=(87)/(2)w^(0)-2w^(1)`

`\frac{\text{d}A}{\text{d}w}=(87)/(2)(1)-2w`

`\frac{\text{d}A}{\text{d}w}=(87)/(2)-2w`

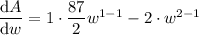
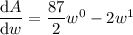
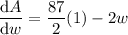
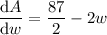
Set dA/dw to zero and solve for w:

`\begin{aligned}(87)/(2)-2w&=0\\\\2w&=(87)/(2)\\\\w&=(87)/(4)\\\\w&=21.75\;\sf m\end{aligned}`

Therefore, the width that maximizes the area of a rectangle with a perimeter of 87 m is 21.75 m.

To find the length, substitute the found value of w into the expression for length (l):

`\begin{aligned}l&=(87)/(2)-(87)/(4)\\\\l&=(87)/(4)\\\\l&=21.75\; \sf m\end{aligned}`

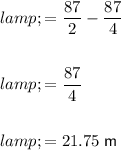
Therefore, the length that maximizes the area of a rectangle with a perimeter of 87 m is 21.75 m.

In conclusion, the dimensions of the rectangle with a perimeter of 87 m than maximize the area are:

• Width = 21.75 m
• Length = 21.75 m
  

This proves that among all rectangles with a fixed perimeter, the square has the maximum area.