Answer:
Option A - Power property
Explanation:
Given : Expression
![\log \sqrt[6]{25x^2}=(1)/(3)\log 5x](https://img.qammunity.org/2018/formulas/mathematics/high-school/bnapajojt3hhibhogdl73chq3ek1ryk0o2.png)
To find : Choose the property used to rewrite the expression?
Solution :
First we rewrite or solve the expression again.
Taking LHS of the given expression and solve,
![LHS=\log \sqrt[6]{25x^2}](https://img.qammunity.org/2018/formulas/mathematics/high-school/1s9fcu2s4jqluvyt3kd4ze4xevxk0f9elv.png)
Solving power by property,
i.e,
![\sqrt[n]{x}=x^{(1)/(n)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/9gglaj088ygwr5207e32pnum6swyi023fv.png)
![=\log [(5x)^2]^(1)/(6)](https://img.qammunity.org/2018/formulas/mathematics/high-school/djxqouo9qts3p5t34jgzhxasprg58dyj22.png)
![=\log [(5x)]^(1)/(3)](https://img.qammunity.org/2018/formulas/mathematics/high-school/5ba1lg6vhd1quk19ps6utxwsdfnk84u42n.png)
Apply logarithmic power property,
i.e,
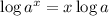
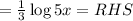
Therefore, The property used to solve the given expression is Power property.
Therefore, Option A is correct.