Question

Choose the property used to rewrite the expression. log ^6sqrt(25x^2)=1/3log5x

A. Power Property

B. Commutative Property

C. Product Property

D. Quotient Property

Answer 1

Option A - Power property

Explanation:

Given : Expression
`\log \sqrt[6]{25x^2}=(1)/(3)\log 5x`

To find : Choose the property used to rewrite the expression?

Solution :

First we rewrite or solve the expression again.

Taking LHS of the given expression and solve,

`LHS=\log \sqrt[6]{25x^2}`

Solving power by property,

i.e,
`\sqrt[n]{x}=x^{(1)/(n)}`

`=\log [(5x)^2]^(1)/(6)`

`=\log [(5x)]^(1)/(3)`

Apply logarithmic power property,

i.e,
`\log a^x=x\log a`

`=(1)/(3)\log 5x=RHS`

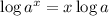
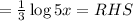
Therefore, The property used to solve the given expression is Power property.

Therefore, Option A is correct.