Answer:
The zeros of the function in the interval of [-2π,2π] are
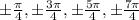 .
.
Explanation:
The given function is
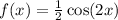
We have to find the zeros of the function in the interval of [-2π,2π].
If
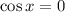 , then
, then
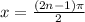
Where n is an integer.
Put f(x)=0, to find the zeroes of the function.
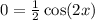
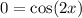
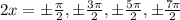
![[\because x\in [-2\pi,2\pi]\Rightarrow 2x\in [-4\pi,4\pi]]](https://img.qammunity.org/2018/formulas/mathematics/college/e5zml6s7669opb43sn5ubb5oi4c2vkmizi.png)
Divide both sides by 2.

Therefore the zeros of the function in the interval of [-2π,2π] are
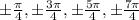 .
.