Question

At a business meeting every person shakes each other's hand once if they were 91 handshakes in total the number of people at the meet is

Answer 1

This is basically asking you to find the number of vertices
`n` of a complete graph that has 91 edges. (I've attached an example of one where
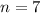
`n=7`, taken from Wiki "complete graph" article)

Let's say you have
`n` unconnected vertices, each labelled with a number
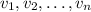
`v_1,v_2,\ldots,v_n` (just for the purpose of tracking which ones you've already taken into account). Draw edges connecting
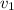
`v_1` to all the other vertices. There are
`n-1` possible edges you can draw.

Now starting from
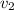
`v_2`, there's already an edge between it and
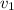
`v_1`, which means there are
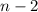
`n-2` other possible edges that you can draw.

Next, from
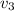
`v_3`, you can only draw
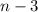
`n-3` new edges because
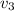
`v_3` is already connected to
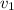
`v_1` and
`v_2`.

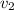
Continuing in this pattern, you find that the second-to-last edge,
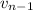
`v_(n-1)` can only be connected once to
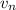
`v_n`, and finally arriving at
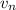
`v_n` you find that all possible connections have been exhausted.

The takeaway here is that the total number of possible connections is the sum


`S=(n-1)+(n-2)+(n-3)+\cdots+1+0`

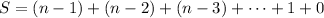
Writing the terms in reverse order, you have


`S=0+1+2+\cdots+(n-2)+(n-1)`

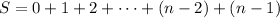
So now if you add up the first, second, ..., terms of the two equivalent sums, you have


`2S=(n-1+0)+(n-2+1)+(n-3+2)+\cdots+(1+n-2)+(0+n-1)`

`2S=(n-1)+(n-1)+(n-1)+\cdots+(n-1)+(n-1)`

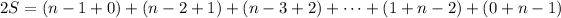
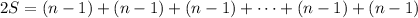
In other words, you're adding up
`n-1`,
`n` times (since each
`n-1` corresponds to a distinct vertex), so you have


`2S=n(n-1)`

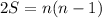
Dividing by 2, you end up with


`S=\frac{n(n-1)}2`

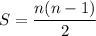
Now, since you know that 91 handshakes took place in total, you have


`91=\frac{n(n-1)}2\implies 182=n(n-1)\implies n=-14,13`

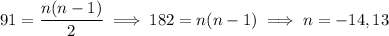
Obviously, we omit the negative solution, so there were 13 people at the meeting.