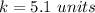Question

CAN SOMEONE PLS HELP?? IM AB TO FAIL GEOMETRY AND NEED HELP W LAW OF SINES. PLEASE

1. In ΔABC, c = 5.4, a = 3.3, and . What are the possible approximate lengths of b? Use the law of sines to find the answer.
2.0 units and 4.6 units
2.1 units and 8.7 units
2.3 units and 7.8 units
2.6 units and 6.6 units
2)What is the approximate value of k? Use the law of sines to find the answer.
2.9 units
3.8 units
5.1 units
6.2 units

please help!!

Answer 1

Part a) In ΔABC, c = 5.4, a = 3.3, and m∠A=20° . What are the possible approximate lengths of b? Use the law of sines to find the answer.

we know that

`(sin\ A)/(a) =(sin\ B)/(b) =(sin\ C)/(c)`

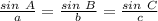
Step
`1`

Find the value of angle C

`(sin\ A)/(a) =(sin\ C)/(c)`

`(sin\ 20)/(3.3) =(sin\ C)/(5.4)\\ \\ sin\ C=(5.4*sin\ 20)/(3.3) \\ \\ sin\ C=0.5597\\ \\ C=arcsin(0.5597)\\ \\ C=34\ degrees`

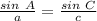
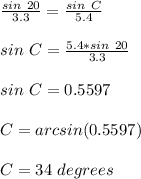
Step
`2`

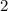
Find the value of angle B

we know that

`A+B+C=180\\ B=180-(A+C)\\ B=180-(20+34)\\ B=126\ degrees`

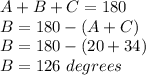
Step
`3`

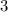
Find the value of side b

`(sin\ A)/(a) =(sin\ B)/(b)`

`(sin\ 20)/(3.3) =(sin\ 126)/(b)\\ \\ b=(3.3*sin\ 126)/(sin\ 20) \\ \\ b=7.8\ units`

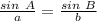
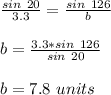
Step
`4`

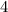
Find the alternative angle C

`C=180-34\\ C=146\ degrees`

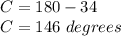
Find the alternative angle B

`A+B+C=180\\ B=180-(A+C)\\ B=180-(20+146)\\ B=14\ degrees`

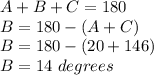
Find the alternative value of side b

`(sin\ A)/(a) =(sin\ B)/(b)`

`(sin\ 20)/(3.3) =(sin\ 14)/(b)\\ \\ b=(3.3*sin\ 14)/(sin\ 20) \\ \\ b=2.3\ units`

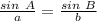
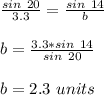
therefore

the answer Part a) is the option

`C:\ 2.3\ units\ and\ 7.8\ units`

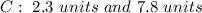
Part b) What is the approximate value of k? Use the law of sines to find the answer

Step
`1`

Find the value of angle J

we know that

`J+K+L=180\\ J=180-(K+L)\\ J=180-(120+40)\\ J=20\ degrees`

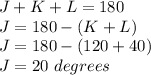
Step
`2`

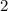
Find the value of side k

`(sin\ K)/(k) =(sin\ J)/(j)`

`(sin\ 120)/(k) =(sin\ 20)/(2)\\ \\ k=(2*sin\ 120)/(sin\ 20) \\ \\ k=5.1\ units`

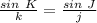
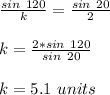
therefore

the answer Part b)

`k=5.1\ units`

Answer 2

The laws of sines is already indicated in the provided images.

1. sin20/3.3 = sinC/5.4
Thus, angle C is 34.03 degrees. To find angle B: 180 - 20 - 34.03 = 126 degrees. Using the law of sines,

sin20/3.3 = sin(126)/b
b = 7.8 units

From this answer, we can already tell that the answer is letter C: 3 units and 7.8 units.

2. Angle J = 180 - 120 - 40 = 20 degrees. Then,

sin(20)/2 = sin(120)/k
k = 5.1 units