The possible values of k for which the x- and y-intercepts of the graph of
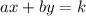 are integers are all multiples of the greatest common divisor (GCD) of a and b.
are integers are all multiples of the greatest common divisor (GCD) of a and b.
1. X-intercept: When the graph intersects the x-axis, y is zero. Substituting y = 0 into the equation ax + by = k, we get ax = k. For the x-intercept to have an integer value, k must be a multiple of the GCD of a.
2. Y-intercept: Similarly, when the graph intersects the y-axis, x is zero. Substituting x = 0 into the equation ax + by = k, we get by = k. For the y-intercept to have an integer value, k must be a multiple of the GCD of (b).
3. Common GCD: To ensure that both x- and y-intercepts have integer values, k must be a multiple of the GCD of both a and b. Therefore, k can take any integer value that is a multiple of GCD (a, b).
In summary, the possible values of k are all integers that are multiples of GCD (a, b).