Question

What else would need to be congruent to show that ABC DEF by SAS?

Answer 1

line BC needs to be congruent to EF

Answer 2

Option C is correct

`\overline{BC} \cong \overline{EF}`

Explanation:

SAS(Side-Angle-Side) postulates states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.

As per the statement:

Given:

`\overline{AC} \cong \overline{DF}`

`\angle C \cong \angle F`

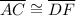
In triangle ABC and DEF.

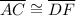`\overline{AC} \cong \overline{DF}` [Side]

`\angle C \cong \angle F` [Angle]

`\overline{BC} \cong \overline{EF}` [Side]

then by SAS postulates we have;

ΔABC≅ΔDEF

Therefore,
`\overline{BC} \cong \overline{EF}` need to be congruent to show that: ΔABC≅ΔDEF