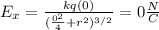Question

A certain electric dipole consists of charges + and − separated by distance , oriented along the -axis as shown in the figure. Find an expression for the magnitude of the electric field of the dipole at a point far away in the -direction, a distance away from the midpoint of the dipole. Assume that is much greater than . Enter your answer in terms of , , , and 0. I've seen one other post about this question but the answer is wrong. I'd really appreciate help on this.

Answer 1

Hi there!

Let's say we have a point 'p' placed at a distance 'r' away from the origin, where r > > d.

The electric field from the +q charge will point towards the top-right, while the electric field from the negative chart will point towards the bottom-right.

Since both charges are of the same magnitude, the y-components will cancel out. We must solve for the x-component of the electric field.

We can begin by deriving an equation for the electric field.

`E= (kq)/(R^2)`

`R = \sqrt{((d)/(2))^2 + r^2}`

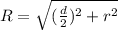
We are solving for E in the x-direction, so:

`E_x = (kq)/(R^2)sin\phi`

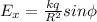
Substitute in the above, and:

`sin\phi = \frac{(d)/(2)}{\sqrt{((d)/(2))^2 + r^2}} = \frac{d}{2\sqrt{(d^2)/(4) + r^2}}`

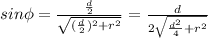
Calculate Ex for one charge:

`E_x= (kq)/((d^2)/(4) + r^2) * \frac{d}{2\sqrt{(d^2)/(4) + r^2}}`

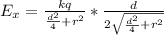
Simplify:

`E_x = (kqd)/(2((d^2)/(4) + r^2)^(3/2))`

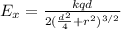
There are two charges, so:

`2E_x = E_x = 2((kqd)/(2((d^2)/(4) + r^2)^(3/2))) = (kqd)/(((d^2)/(4) + r^2)^(3/2))`

To find the field if r > > d, we can begin by factoring out r² from inside the parenthesis:

`E_x = (kqd)/(((d^2)/(4) + r^2)^(3/2)) \\ \\ =(kqd)/(r^3((d^2)/(4r^2) + 1)^(3/2))`

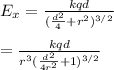
Terms with d/r go to 0, so:

`(d)/(r^3) = 0 \\ \\ (d^2)/(4r^2) = 0`

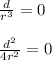
So:

`E_x =(kq(0))/((0 + 1)^(3/2)) = \boxed{0 (N)/(C)}`

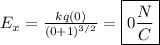
**We can also think of this situation as d ≈ 0. As the 'r' increases and becomes MUCH greater than 'd', the charges appear to be right next to one another (d ≈ 0). If we plug in d = 0 into our equation:

`E_x =(kq(0))/(((0^2)/(4) + r^2)^(3/2)) = 0 (N)/(C)`