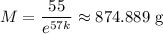Given that the half-life of the sample is 14.28 days, you are looking for a decay factor
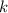
such that
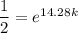
Solving for
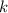
yields
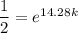
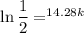
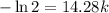
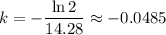
Now, after 57 days, you're told that a sample of unknown mass decayed to 55g, which means if
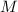
was the starting mass of the sample, then
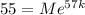
Solving for
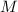
yields