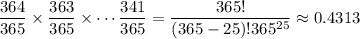Question

Find the probability that of 25 students, no two have the same birthday

Answer 1

Assuming no student was born on Leap Day, and that birthdays are as likely to occur on one day as any other, each student has
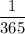
`\frac1{365}` probability of being born on a particular day. So if one student's birthday was, say, 1 January, the probability that another student was born on 2 January is
`(364)/(365)`.

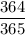
The probability, then, of having the next student born on 3 Januaray is
`(363)/(365)`.

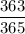
Continuing in this fashion, for 25 students you would find that no two share a birthday with probability


`(364)/(365)*(363)/(365)*\cdots(341)/(365)=(365!)/((365-25)!365^(25))\approx0.4313`