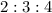Answer:
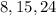
Explanation:
In this problem we have a ratio with
 numbers
numbers
so
Let
x------> the first number
y-----> the second number
z-----> the third number
we know that
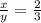 ------> equation A
------> equation A
 ------> equation B
------> equation B
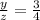 ------> equation C
------> equation C
Verify each case
case A)
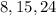
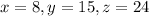
Substitute in the equations
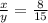
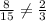
therefore
The case A) not have a ratio of
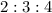
case B)
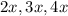

Substitute in the equations
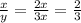
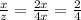
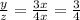
therefore
The case B) have a ratio of
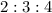
case C)
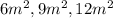
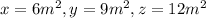
Substitute in the equations
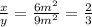
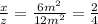
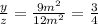
therefore
The case C) have a ratio of