Question

A chessboard has 64 squares. George places 1 grain of rice on the first square, 2 grains on the second square, 4 grains on the third square, 8 grains on the fourth square, and so on, until he has placed grains of rice on 10 squares. Once George has put rice on the 10th square, he has placed a total of (how many) grains of rice on the chess board.

Answer 1

The number of grains on the Nth square Is 2^(N-1). There are 512 grains on the 10th square alone, and 1,023 of them on all 10 squares together.

Answer 2

Answer: There are 1023 grains on 10 squares in total.

Explanation:

Since we have given that

Number of grains on first square = 1

Number of grains on second square = 2

Number of grains on third square = 4

Number of grains on fourth square = 8

Since it forms a geometric sequence :

1,2,4,8,......................

So, we need to find the number of squares on 10 th square:

So, here, a = 1

r = 2

n = 10

`S_(10)=(a(r^(n-1)))/(r-1)\\\\S_(10)=(1(2^(10-1)))/(2-1)\\\\S_(10)=1024-1\\\\S_(10)=1023`

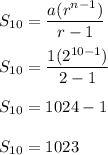
Hence, there are 1023 grains on 10 squares in total.