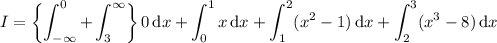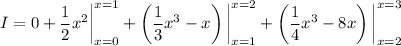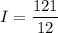Question

Just confused! Why we split abs definite integrand/integration at zero although it is continuos there? Please anyone help me.

Answer 1

Suppose you want to compute the integral


`\displaystyle\int_a^b|x|\,\mathrm dx`

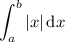
where
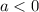
`a<0` and
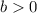
`b>0`. Recall the definition of the absolute value function:


`|x|=\begin{cases}x&\text{for }x\ge0\\-x&\text{for }x<0\end{cases}`

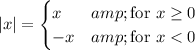
What this means is that the function has a different meaning depending on the domain from which
`x` is picked (the two domains being non-negative and negative real numbers). For non-negative numbers
`x`, you have
`|x|=x` exactly, while if
`x` is negative, you have
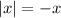
`|x|=-x` exactly.

Choosing between
`|x|=x` and
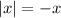
`|x|=-x` is then determined by the "turning point"
`x=0`. Because the function behaves differently at values to either side of this point, you essentially have two different integrands to consider.

So, to compute the integral above, you would split the interval of integration at
`x=0` and use the appropriate definition for
`|x|`.


`\displaystyle\int_a^b|x|\,\mathrm dx=\int_a^0(-x)\,\mathrm dx+\int_0^bx\,\mathrm dx`

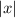
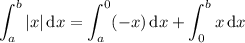
which comes from the linearity property of definite integrals, and the fact that the interval
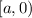
`[a,0)` contains only negative numbers, while
`(0,b]` contains only positive numbers.

Then, carry on with the integration:


`\displaystyle\int_a^0(-x)\,\mathrm dx+\int_0^bx\,\mathrm dx=-\frac12x^2\bigg|_(x=a)^(x=0)+\frac12x^2\bigg|_(x=0)^(x=b)=-\frac12(0^2-a^2)+\frac12(b^2-0^2)=\frac{b^2+a^2}2`

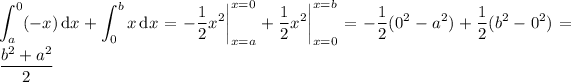
Edit: The key here is that
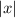
`|x|` is a piecewise function, i.e. a function that basically takes on the role of potentially completely different functions. In the case of
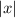
`|x|`, there are two possible equivalences,
`x` and
`-x`.

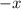
Splitting up the domain of integration is a requirement for computing integrals of piecewise functions. Take for another example the function


`f(x)=\begin{cases}x&\text{for }0\le x\le 1\\x^2-1&\text{for }1< x\le2\\x^3-8&\text{for }2< x\le3\\0&\text{otherwise}\end{cases}`

and let's say we want to compute the integral


`I=\displaystyle\int_(-\infty)^\infty f(x)\,\mathrm dx`

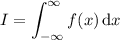
How is this done? Well, you have to split up the domain of integration because
`f(x)` doesn't have the same meaning everywhere in its domain:


`I=\left\{\displaystyle\int_(-\infty)^0+\int_0^1+\int_1^2+\int_2^3+\int_3^\infty\right\}f(x)\,\mathrm dx`

`I=\displaystyle\left\{\int_(-\infty)^0+\int_3^\infty\right\}0\,\mathrm dx+\int_0^1x\,\mathrm dx+\int_1^2(x^2-1)\,\mathrm dx+\int_2^3(x^3-8)\,\mathrm dx`

`I=\displaystyle0+\frac12x^2\bigg|_(x=0)^(x=1)+\left(\frac13x^3-x\right)\bigg|_(x=1)^(x=2)+\left(\frac14x^3-8x\right)\bigg|_(x=2)^(x=3)`

`I=(121)/(12)`