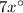we know that
The sum of the internal angles of the triangle is equal to
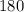 degrees
degrees
in this problem we have
m∠2=
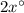
m∠3=
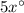
m∠1+m∠2+m∠3=
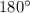
Substitute the values and solve for m∠1
m∠1=
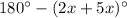
m∠1=

Remember that
m∠1+m∠4=
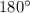 -------> by supplementary angles
-------> by supplementary angles
Substitute the value of m∠1 and find m∠4
m∠4=
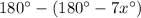
m∠4=
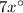
therefore
the answer is
a) the measure of m∠1=

b) the measure of m∠4=