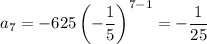Question

What is the 7th term of the geometric sequence where a1 = -625 and a2 = 125

Answer 1

-0.04 is the answer

Explanation:

Answer 2

Since the sequence is geometric, there is some constant
`r` such that the sequence is recursively given by


`a_n=ra_(n-1)`

By this definition, you can recursively substitute into the right hand side the definition for
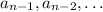
`a_(n-1),a_(n-2),\ldots` to find an explicit formula for the
`n`th term.


`a_n=ra_(n-1)=r^2a_(n-2)=r^3a_(n-3)=\cdots=r^(n-1)a_1=-625r^(n-1)`

You know the second term, which means you can find
`r`:


`a_2=-625r^(2-1)\implies125=-625r\implies r=-\frac15`

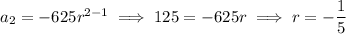
So, the 7th term of the sequence is


`a_7=-625\left(-\frac15\right)^(7-1)=-\frac1{25}`