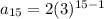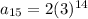Answer:
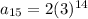
Explanation:
the sequence 2, 6, 18, 54, ...,
3 is multiplied with first term to get 6
2*3 = 6
6* 3= 18
18 * 3= 54
Each term is multiplied with 3 to get next term
Given sequence is geometric
To get nth term we use formula
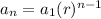
Where 'a1' is the first term
r is the common ratio
n is the number of terms
first term a1= 2
Each term is multiplied with 3 to get next term, so r= 3
now we need to find out the fifteenth term so n= 15