This is a linear relationship. The slope-intercept form of the linear equation is:
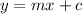
Where,
- m is the rate of change (positive if increasing rate and negative if decreasing rate)
- c is the y intercept, or the initial value
Rate of change is 2.5 quarts per minute (it is decreasing so m is -2.5)
Initial value is 50 quarts, so c is 50.
Plugging in the values we get
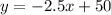 .
.
Changing variables to w instead of y and t instead of x, gives us,
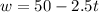 . Where w is warts of water left in the tub and t is the time in minutes.
. Where w is warts of water left in the tub and t is the time in minutes.
There is no viable solution when t=30 because at t=20, w=0 (
 ). It means after 20 minutes, there is no water left. So t=30 minutes doesn't make sense.
). It means after 20 minutes, there is no water left. So t=30 minutes doesn't make sense.
ANSWER:
Modelling equation:
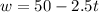
When
 , there is no VIABLE solution
, there is no VIABLE solution