Answer:
1/(x^2 +6x)
Explanation:
The denominators used in your difference must have factors of x, (x-6), and (x +6). The only two tiles that have denominator factors on this list are the one you found, (x+2)/(x^2 -36), and the middle remaining one:
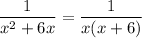
Your difference is ...
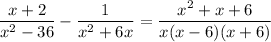
__
You can work out the sum on the left side to verify this.
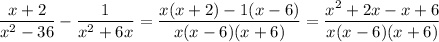
Combining the two 'x' terms in the numerator of the last expression on the right gives the desired result.