Answer:
15 minutes.
Explanation:
Let x represent the distance from home to school.
Kris runs half of the distance to school averaging 6 mph.
Time = Distance/speed
Time taken to cover the half distance (x/2) at a rate of 6 mph would be:
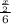
He jogs the rest of the way to school averaging 4 mph. Time taken to cover the half distance (x/2) at a rate of 4 mph would be:
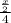 .
.
Time taken to complete the distance (x) is 25 minutes.
Speed is miles pr hour, so we need to convert time from minutes to hours as:
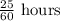
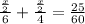
Using
 , we will get:
, we will get:
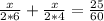
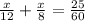
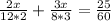
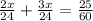
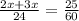
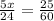
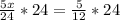
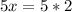
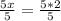
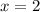
Therefore, the distance between Kris's home and school is 2 miles.
Time = Distance/speed
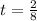
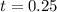
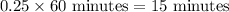
Therefore, it will take 15 minutes for Kris to reach home.