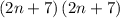Answer:
Factor of Equation
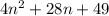 is
is
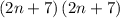
Explanation:
Given : Equation
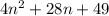
We have to factorize the given equation completely.
Consider the given equation
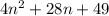
We can rewrite
 , we get,
, we get,
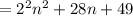
We can rewrite
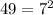 , we get,
, we get,
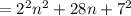
Apply exponent rule,
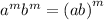
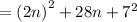
Apply identity,
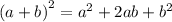 ,we get,
,we get,
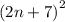
Thus, Factor of Equation
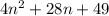 is
is