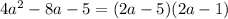Question

Factor completely and then place the factors in the proper location on the grid. 4a 2 - 8a - 5

Answer 1

(2a - 5)(2a + 1)
Again proper order?

Answer 2

Answer:
`(2a-5)(2a-1)`

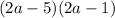
Explanation:

Given quadratic polynomial:
`4a^2-8a-5`

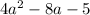
To factorize the given quadratic polynomial we use the "splitting of middle term" method that is the x term which is the sum of two factors and product equal to last term.

The product of first and last term =
`4a^2*(-5)=-20a^2`

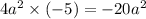
The middle term of the given polynomial can be written as

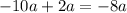`-10a+2a=-8a`, where -10a and 2a are the factors of
`-20a^2`.

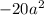Now,
`4a^2-8a-5\\=4a^2-10a+2a-5\\2a(2a-5)+1(2a-5)\\(2a-5)(2a-1)`

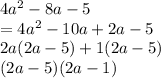
Hence,
`4a^2-8a-5=(2a-5)(2a-1)`