kx-y≥x+z
minus x both sides
kx-x-y≥z
add y to both sides
kx-x≥y+z
undistribute x
x(k-1)≥y+z
divide both sides by (k-1)
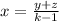
if k is greater than 1, then the denomenator is positive, then x is positive (assuming z+y is positive)
if k is les than 1, the the denomenator is negatve, then x is negative
if k is equal to 1, then x is undefined