Answer:
Height of building is 76 feet.
Explanation:
In the figure below,
AB is the building , DE is the tree standing in half way between the state and building.
Let angle at C be

In ΔABC,
tan
 =
=
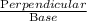
tan
 =
=
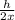 ......(1)
......(1)
In ΔDEC,
tan
 =
=
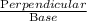
tan
 =
=
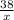 ......(2)
......(2)
Comparing (1) and (2) ,
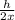 =
=
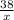
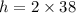
⇒
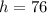
Thus, Height of building is 76 feet.