Question

For which of the following values of m would the system of equations y=4x+1 and y=mx-5 have no solution?

A)4
B)1
C)-5
D)-4

Answer 1

Option A - m=4

Explanation:

Given : Equation
`y=4x+1,y=mx-5`

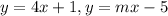
To find : For which of the following values of m would the system of equations have no solution ?

Solution :

When the system of equation is in form
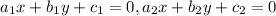`a_1x+b_1y+c_1=0, a_2x+b_2y+c_2=0` then the condition for no solutions is

`(a_1)/(a_2)=(b_1)/(b_2)\\eq (c_1)/(c_2)`

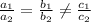
Re-write equation as
`4x-y+1=0,mx-y-5=0`

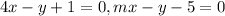
Comparing with given equations,

`a_1=4, b_1=-1,c_1=1\text{ and }a_2=m, b_2=-1,c_2=-5`

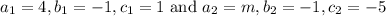
Substituting the values,

`(4)/(m)=(-1)/(-1)\\eq (1)/(-5)`

`(4)/(m)=(1)/(1)\\eq -(1)/(5)`

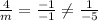
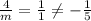
Taking first two equation,

`(4)/(m)=(1)/(1)`

`m=4`

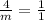
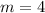
Therefore, The value of m is 4.

So, Option A is correct.

Answer 2

I believe the correct answer from the choices listed above is option A. It would be 4 that would make the system of equations y=4x+1 and y=mx-5 to have no solution. It will make them parallel lines where they do not intersect at any point.