Question

What are the coordinates of the circumcenter of a triangle with vertices A(−1,1), B(5,1), and C(−1,−1)? Enter your answer in the boxes.

Answer 1

Explanation:

Answer 2

Circumcenter is (2,0)

Explanation:

We have been given three vertices of a triangle A(-1,1), B(5,1) and C(-1,-1)

The triangle formed by these vertices is a right angle triangle you can see the attachment for the figure

To Prove the vertices form right angle triangle we can satisfy the pythagoras theroem which says that square of hypotenuse is equal to sum of square of sides.

Here hypotenuse Hypotenuse is BC which is the longest side

Hence
`(BC)^2=(AB)^2+(AC)^2`

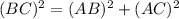
Hence find the distance of BC using distance formula which is

`Distance=√((x_2-x_1)^2+((y_2-y_1)^2)`

Substituting the value B(5,1) and C(-1,-1) in the distance formula

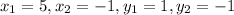`x_1=5,x_2=-1,y_1=1,y_2=-1` we will get

`BC=√((-1-5)^2+(-1-1)^2)`

`\RightarrowBC=\sqrt{(-6)^2+(-2)^2`

`\RightarrowBC=√(36+4)`

`\RightarrowBC=√(39)`

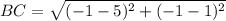
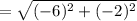
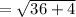
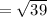
Similarly, we will find AB with
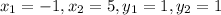`x_1=-1,x_2=5,y_1=1,y_2=1`we will get

`AB=\sqrt{(5+1)^2+(1-1)^2`

`\RightarrowAB=√(36)`

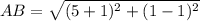
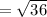
Similarly, we will find AC

Here,
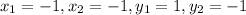`x_1=-1,x_2=-1,y_1=1,y_2=-1`substituting values in the formula we will get

`AC=√((-1-(-1))^2+(-1-1)^2)`

`\RightarrowAC=\sqrt{(-1+1)^2+(-2)^2`

`\RightarrowAC=\sqrt{(0)+4`

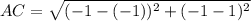
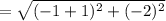
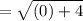
Hence,
`(BC)^2=(AB)^2+(AC)^2`

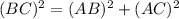
Implying the triangle is right angle triangle

And circumcenter of right angle triangle is mid point of hypotenuse.

Now, we will find midpoint of hypotenuse that is midpoint of BC

`\text{Midpoint formula}=\left ( (x_1+x_2)/(2),(y_1+y_2)/(2) \right )`

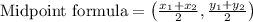
Here,
`x_1=5,x_2=-1,y_1=1,y_2=-1`

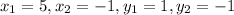
On substituting the values in the formula we will get

`\text{Midpoint formula (x,y)}=(5+(-1))/(2),(1+(-1))/(2)`

`\Rightarrow(4)/(2),(0)/(2)`

`\Rightarrow(2,0)`

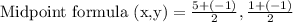
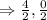
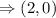
Hence, circumcenter is (2,0)