Question

Use Pythagorean identities to prove whether ΔLMN is a right, acute, or obtuse triangle. Show all work for full credit.

Answer 1

Answer: The given triangle LMN is an obtuse-angled triangle.

Step-by-step explanation: We are given to use Pythagorean identities to prove whether ΔLMN is a right, acute, or obtuse triangle.

From the figure, we note that

in ΔLMN, LM = 5 units, MN = 13 units and LN = 14 units.

We know that a triangle with sides a units, b units and c units (a > b, c) is said to be

(i) Right-angled triangle if
`b^2+c^2=a^2,`

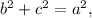
(ii) Acute-angled triangle if
`b^2+c^2>a^2,`

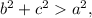
(iii) Obtuse-angled triangle if
`b^2+c^2<a^2.`

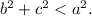
For the given triangle LMN, we have

a = 14, b = 13 and c = 5.

So,

`b^2+c^2=13^2+5^2=169+25=194,\\\\a^2=14^2=196.`

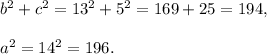
Therefore,
`b^2+c^2<a^2.`

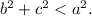
Thus, the given triangle LMN is an obtuse-angled triangle.