Question

HELP PLASE<3

The graph of f(x) = |x| has been stretched by a factor of 2.5. If no other transformations of the function have occurred, which point lies on the new graph?


A. ( –4, –4)

B. (–3, 7.5)

C. ( –2, 5.5)

D.( –1, –2.5)

Answer 1

The answer is B (-3, 7.5) 

Answer 2

Option B is correct.

The point which lies on the new graph g(x) is, (-3, 7.5)

Explanation:

For a base function f(x), a new function g(x) = cf(x) is vertically stretched by a factor c if c> 1.

Given the parent function: f(x) =|x|

Now, by vertically stretched definition,

A function f(x) is vertically stretched by a factor of 2.5 then; we have the new function or new graph i.e,

g(x) = 2.5 f(x) where c=2.5 > 1

therefore, g(x) =2.5|x|

We have to find which point lies on the new graph;

Option A:

(-4 , -4)

Here x = -4 and g(-4) = -4

`g(-4) = 2.5 |-4|`

`-4=2.5 \cdot 4=10`

-4 = 10 False.

Option B:

(-3 , 7.5)

g(x) = 2.5|x|

`g(-3) = 2.5 |-3|`

`7.5= 2.5 \cdot 3=7.5`

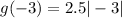
7.5 = 7.5 True.

Option C:

(-2 , 5.5)

`g(-2) = 2.5 |-2|`

`5.5 = 2.5 \cdot 2=5`

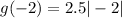
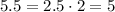
5.5 = 2 False.

Option D:

(-1 , -2.5)

`g(-1) = 2.5 |-1|`

`-2.5 = 2.5 \cdot 1=2.5`

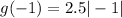
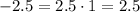
-2.5 = 2.5 False

Therefore, from above you can see that the only point which is true for the new graph is, (-3 , 7.5)