Question

Telephone signals are often transmitted over long distances by microwaves. what is the frequency of microwave radiation with a wavelength of 3.5 cm ?

Answer 1

`0.86* 10^(10) Hz`

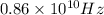
Step-by-step explanation:

Given that, the wavelength of the microwave radiation is,

`\lambda=3.5 cm=3.5* 10^(-2)m`

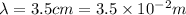
And as we know that the speed of the wave is,

`v=3* 10^(8)m/s`

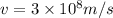
Now the frequency of the microwave radiation can be calculated as

`f=(v)/(\lambda)`

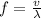
Here, f is the frequency of microwave signal, v is the speed of the signal and
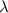`\lambda` is the wavelength of signal.

Now put all the given variable in above equation.

`f=(3* 10^(8)m/s)/(3.5* 10^(-2)m ) \\f=0.86* 10^(10) Hz`

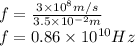
This the required frequency.

Answer 2

Microwaves move at the speed of light which is equal to 3 x 10^8 m/s. The frequency of a wave is calculated by dividing its speed by the wavelength. Through that approach,
f = (3x10^8 m/s)(100 cm/1m) / 3.5 cm
= 8571428571/s = 8 571 MHz