Question

Five times the number of test tubes in a school’s chemistry lab exceeds three times the number of beakers it has by 660. The sum of two times the number of test tubes and five times the number of beakers is 450, If b is the number of beakers and t is the number of test tubes, the system of linear equations representing this situation is ...

The number of beakers in the school’s lab is ... and the number of test tubes in the school’s lab is...

Answer 1

Answer
Beakers: 30
Test tubes: 150

Answer 2

The numbers of test tubes are 150 and beakers are 30.

Explanation:

we have to find numbers of beaker ans test tubes in chemistry lab

Given statement is "Five times the number of test tubes in a school’s chemistry lab exceeds three times the number of beakers it has by 660. The sum of two times the number of test tubes and five times the number of beakers is 450"

Let the number of beakers be b

and Let the number of test tubes be t

According to question

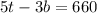`5t-3b=660` ......(1)

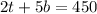`2t+5b=450` ......(2)

solve linear equation by substitution method,

isolate the b in equation (1)

`5t-3b=660`

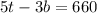
subtract both the sides by 5t,

`-3b=660-5t`

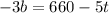
divide both the sides by -3,

tex]b=\frac{5t-660}{3}[/tex]

substitute the value of b in equation (2)

`2t+5((5t-660)/(3))=450`

`2t+((25t-3300)/(3))=450`

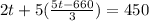
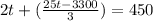
multiply both the sides by 3,

`6t+25t-3300=1350`

`31t-3300=1350`

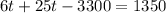
Add both the sides by 3300,

`31t=1350+3300`

`31t=4650`

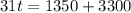
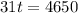
divide both the sides by 31,

`t=150`

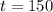
the numbers of test tubes are 150.

Put the value of t in equation (1)

`5t-3b=660`

`5(150)-3b=660`

`750-3b=660`

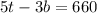
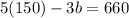
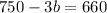
subtract both the sides by 750,

`-3b=660-750`

`-3b=-90`

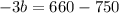
divide both the sides by -3,

`b=30`

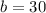
the numbers of beakers are 30.

Therefore, the numbers of test tubes are 150 and beakers are 30.