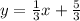Question

write the slope intercept form of an equation of the line that passes through (4,3) that is perpendicular to the line Y=-3x-15

Answer 1

If two lines are perpendicular, then their slopes have a product of -1 or you could say they are opposite signed reciprocals of each other.
The given equation has a slope of -3. We know this because it is in slope-intercept form y = mx + b ...y = (slope)x + (y-intercept).

so taking the slope -3...the opposite signed reciprocal would be +
`(1)/(3)`

Now we have a slope and a point... we can use them to find the b (y-intercept)
x = 4, y = 3, and m =
`(1)/(3)`

`3= (1)/(3) (4)+b`

`3= (4)/(3) +b`
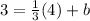
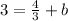
Using the common denominator fraction for 3, we subtract 4/3 from both sides

`3= (9)/(3)`

`(5)/(3) =b`
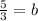
plug the values for m and b into the slope intercept form

`y= (1)/(3) x+ (5)/(3)`