Question

If the equation of an ellipse is in standard form and the denominators are equal, then the ellipse is a circle. True or False?

Answer 1

The statement is a TRUE statement.

Explanation:

We know that the standard form of an ellipse is given as:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

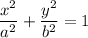
where a and b are the x and y-intercepts respectively.

Also when the denominator i.e. a=b then,

`(x^2)/(a^2)+(y^2)/(a^2)=1\\\\\\x^2+y^2=a^2`

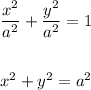
Hence, we get the general equation of a circle whose center is at the origin and radius is 'a' or 'b' units.

Hence, the statement:

If the equation of an ellipse is in standard form and the denominators are equal, then the ellipse is a circle is a TRUE statement.

Answer 2

I believe the correct answer is true. If the equation of an ellipse is in standard form and the denominators are equal, then the ellipse is a circle. The equation of the ellipse in this case will reduce to an equation of a circle. Hope this answers the question. Have a nice day.