Answer:
The required range of the function
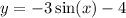 is [-7,-1]
is [-7,-1]
Explanation:
Given : Function
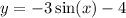
To find : What is the range of the given function?
Solution :
The range is defined as the variation in which any function is defined.
We know that the sin function lies between [-1,1]
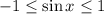 .....(1)
.....(1)
The required function is
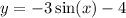
Multiply equation (1) by -3
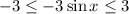 .....(2)
.....(2)
Now, we subtract equation (2) by 4
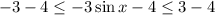
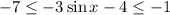
Therefore, The required range of the function
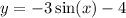 is [-7,-1].
is [-7,-1].