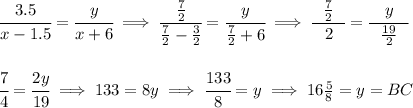Question

9. ABC and DEF are similar triangles. Find the measure of BC.
Please help! ​

Answer 1

Check the picture below.

let's change the decimal amounts to fractions, so for 3.5 let's use 7/2 and for 1.5 let's use 3/2, let's use the proportion on the left side and then the next one after

`\cfrac{3.5}{2x+7}=\cfrac{x-1.5}{8}\implies \cfrac{~~ (7)/(2)~~}{2x+7}=\cfrac{x-(3)/(2)}{8}\implies \cfrac{~~ (7)/(2)~~}{(2x+7)/(1)}=\cfrac{(2x-3)/(2)}{(8)/(1)} \\\\\\ \cfrac{7}{2}\cdot \cfrac{1}{2x+7}=\cfrac{2x-3}{2}\cdot \cfrac{1}{8}\implies \cfrac{7}{4x+14}=\cfrac{2x-3}{16} \\\\\\ 112=8x^2-12x+28x-42\implies 0=8x^2+16x-154 \\\\\\ 0=2(4x^2+8x-77)\implies 0=4x^2+8x-77\implies 0=(2x-7)(2x+11) \\\\\\ 7=2x\implies \boxed{\cfrac{7}{2}=x}`

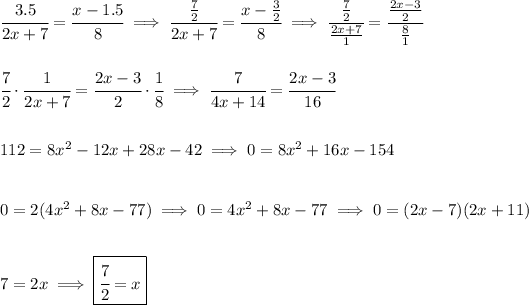
now, let's notice that we didn't use the 2x+11, since that gives us a negative "x" and "x" cannot be a negative value.

`\cfrac{3.5}{x-1.5}=\cfrac{y}{x+6}\implies \cfrac{~~(7)/(2)~~}{(7)/(2)-(3)/(2)}=\cfrac{y}{(7)/(2)+6}\implies \cfrac{~~ (7)/(2)~~}{2}=\cfrac{y}{~~(19)/(2)~~} \\\\\\ \cfrac{7}{4}=\cfrac{2y}{19}\implies 133=8y\implies \cfrac{133}{8}=y\implies 16(5)/(8)=y=BC`