Question

If you shift the quadratic parent function, f(x) = x2, left 12 units, what is the equation of the new function? A.g(x) = (x + 12)2 B.g(x) = (x – 12)2 C.g(x) = x2 – 12 D.g(x) = x2 + 12

Answer 1

f(x) = (x + 12)2

Explanation:

A P E X

Answer 2

Answer: The correct option is (A).
`g(x)=(x+12)^2.`

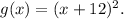
Step-by-step explanation: Given that the equation of the quadratic parent function is

`f(x)=x^2~~~~~~~~~~~~~~~~~~~~~~~~``(i)`

We are to find the equation of the new function after shifting the parent function (i) 12 units left.

Since we are shifting 12 units left, so there is a horizontal translation in the X-axis.

And the x co-ordinate becomes (x+12).

Therefore, the equation of the new function will be

`g(x)=(x+12)^2.`

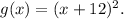
Thus, the required equation of the new function is
`g(x)=(x+12)^2.`

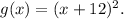
Option (A) is correct.