Answer:
Option: A is the correct answer.
A. P(A | C) = 0.16, P(A) = 0.16, the events are independent
Explanation:
We know that two events A and B are said to be independent if:
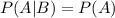
(
Since, we know that if A and B are two independent events then

and:
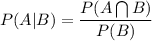
and hence using property (1) we get:
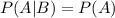 )
)
from the given table we have:
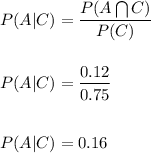
and also, P(A)=0.16
As P(A|C)=P(A)
Hence, events A and C are independent.
Also we may observe that:
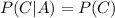
(
Since, from table we have:
P(C)=0.75
and
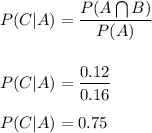 )
)
Hence, events A and C are independent.