Question

If a function has a verticale asymptote at a certain x-value, then the function is at the value

Answer 1

We conclude that If a function has a vertical asymptote at a certain x-value, then the function is undefined at the value.

Explanation:

If a function has a vertical asymptote at a certain x-value, then the function is undefined at the value.

For example, let the function

`f\left(x\right)\:=(x+3)/(x-3)`

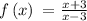
It is clear that the given function becomes undefined at x = 3 in the denominator.

i.e. 3-3 = 0

It means, the function can not have x = 3, otherwise, the function will become undefined.

In other words, if the function has a vertical asymptote at x = 3, then the function is undefined at the value.

Therefore, we conclude that If a function has a vertical asymptote at a certain x-value, then the function is undefined at the value.