Question

A small combination lock on a suitcase has 55 ​wheels, each labeled with the 10 digits 0 to 9. How many 55 digit combinations are possible if successive digits must be​ different?

Answer 1

Suppose
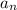
`a_n` is the number of possible combinations for a suitcase with a lock consisting of
`n` wheels. If you added one more wheel onto the lock, there would only be 9 allowed possible digits you can use for the new wheel. This means the number of possible combinations for
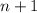
`n+1` wheels, or
`a_(n+1)` is given recursively by the formula


`a_(n+1)=9a_n`

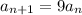
starting with
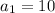
`a_1=10` (because you can start the combination with any one of the ten available digits 0 through 9).

For example, if the combination for a 3-wheel lock is 282, then a 4-wheel lock can be any one of 2820, 2821, 2823, ..., 2829 (nine possibilities depending on the second-to-last digit).

By substitution, you have


`a_(n+1)=9a_n=9^2a_(n-1)=9^3a_(n-2)=\cdots=9^na_1=10*9^n`

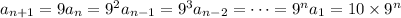
This means a lock with 55 wheels will have


`a_(55)=10*9^(54)`

possible combinations (a number with 53 digits).