Question

Solve the system by the elimination method. check your work. x - 3y = 0 3y - 6 = 2x {(-6, -1/2)} {(-6, -2)} {(-2, -6)}

Answer 1

Doing process of elimination can take a long time, especially if you do not have answers to chose from.
I would start by getting x by itself in one of the equations. The easiest way to go about doing this is changing x - 3y = 0 to
x = 3y.
Now that we know that x equals 3y, we can replace all the x's in the other equation with 3y. This makes the equation
3y - 6 = 2(3y), now we need to combine like terms. Multiply 2 and 3y, to get 3y - 6 = 6y, and then subtract 3y from both sides to get -6 = 3y. Divide both sides by 3, and then get that -2 = y in other words y = -2. After you know what y equals, plug y into one of the equations and solve for x. I did
x - 3(-2) = 0. Multiply -3 by -2, and get x - 6 = 0. Then add six to both sides and then you get that x = 6.
Plug both values into the equation to check the answer. (:

Answer 2

the solution of the given system of equation is {(-6,-2)}

Explanation:

The system of equations is given by

`x-3y=0...(i)\\\\3y-6=2x...(ii)`

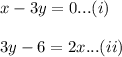
Solve the equation (i) for x

`x-3y=0\\\\x=3y`

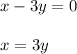
Substitute this value of x in equation (ii) and solve for y

`3y-6=2\cdot3y\\\\3y-6=6y\\\\-3y=6\\\\y=-2`

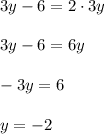
Plugging this value of y in the equation x = 3y

`x=3\cdot(-2)\\\\x=-6`

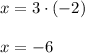
Therefore, the solution of the given system of equation is {(-6,-2)}

Check the solution:

Substitute the value of x and y in original equations

For equation (i)

`x-3y=0\\\\-6-3(-2)=0\\\\-6+6=0\\\\0=0`

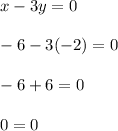
For equation (ii)

`3(-2)-6=2(-6)\\\\-6-6=-12\\\\-12=-12`

We got true results for both the equations.

Hence, the solution is correct.

Therefore, the solution of the given system of equation is {(-6,-2)}